대조군 설정이 불가능한 상황에서 마케팅(처치)에 대한 성과 측정 - 개별 매체의 영향도 비중 평가
WHY?
앞선 포스팅(https://gunlyungyou.github.io/third/)에서는 집행한 마케팅에 대한 전반적인 성과를 측정하는 방법에 대해서 알아보았습니다. 저희 조직에서는 구글, 페이스북, 트위터 등 매체를 이용한 광고 뿐만 아니라 App Push, E-Mail, SMS 등 다양한 수단을 마케팅에 이용하고 있습니다. 이러한 다양한 마케팅 매체의 개별 영향도 평가에 대한 니즈가 있었고 Media-Mix-Modeling을 이용하여 해당 문제를 해결하기로 하였습니다.
What is MMM?
Media-Mix-Modeling은 흔히 Marketing-Mix-Modeling으로도 불리며 집행된 매체의 성과 비중을 파악하기 위한 계량경제모형의 일종입니다. 따라서, 계량경제모형에서 주로 사용하는 regression 모형을 사용하여 Coefficient를 추정하고 이를 각 매체의 영향도로 이용하게 됩니다. regression을 이용하기 때문에 통제 변수에 대한 개념이 적용되며, 이는 특정 조건들을 만족시킨다면 인과 효과적인 측면의 해석에 대한 가능성을 내포하고 있습니다.
그렇다면 MMM이 필요한 이유는 무엇일까요? 보통 마케터분들이 마케팅 성과를 측정하는데 이용하는 클릭과 같은 conversion은 last touch에 대한 한계를 갖고 있습니다. 예를 들어서 특정 유저가 다음과 같은 경로를 통해 광고를 클릭하였고 웹페이지에 유입되었다고 가정해보겠습니다.
TV CF-> Facebook banner -> Youtube video -> Google banner(Click!)
last touch attribution의 방식으로 해당 고객에 대한 마케팅 성과를 측정하면, 이 전환은 Google banner가 가져가게 됩니다. 즉, 이전까지 노출되었던 매체들의 영향은 모두 무시된 채 가장 마지막에 클릭한 매체만의 성과로 잡히게 되는 것입니다. MMM은 이러한 한계를 극복하고자 1970년대에 처음으로 개념이 등장하였고 컴퓨팅 파워가 증가하고 더 오래, 더 다양한 데이터를 이용할 수 있는 현재에 들어서 연구가 활발히 진행되고 있습니다. MMM의 핵심 아이디어를 다음의 그림 한장으로 표현이 가능합니다.
MMM은 크게 아래의 데이터들을 사용하여 모델링을 진행하게 됩니다.
- 광고 지표: 매체별 비용, 노출, 클릭 등
- 마케팅 지표: promotion, 제품 가격, 이벤트 정보 등
- 보정 변수: 계정설, 날씨, 경쟁사 매출 등
자세한 방법론 소개는 실제 집행되었던 광고 캠페인에 대한 분석 결과를 바탕으로 설명하겠습니다.
Case Study
Feature Selection
올해 초 넥슨에서는 신규 서비스 런칭을 위한 사전 예약 캠페인을 진행하였습니다. 해당 캠페인은 저희 조직에서 주로 진행하였으며 구글, 페이스북을 비롯한 총 8개의 매체를 활용하여 캠페인을 진행하였습니다. 보통 MMM은 종속 변수로 매출을 이용하는데 이번에 진행한 캠페인은 사전 예약 캠페인이기 때문에 종속 변수를 “사전예약자 수”로 이용하였습니다.
사전예약자는 아무리 광고를 많이 집행한다고 하더라도 시간이 지남에 따라 자연적으로 감소할 수 밖에 없는 count 데이터입니다. 이러한 데이터를 흔히 포아송 분포를 따른다고 하며, 실제로 일별 사전예약자 수에 대한 분포를 시각화하면 람다가 2정도 되는 포아송 분포를 따르고 있음을 확인할 수 있었습니다.
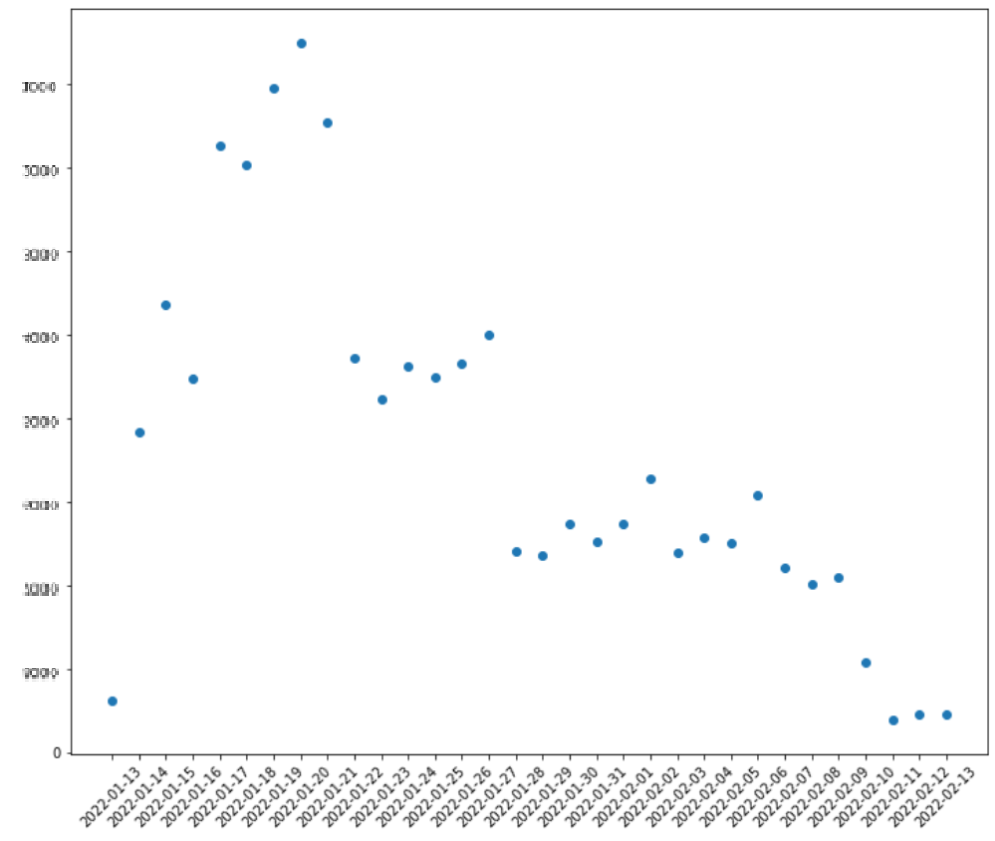
따라서 사전예약자를 종속 변수로하는 모델은 Generalized Linear Model(GLM)을 선택하였고, 그 중에서도 Poisson regression을 이용하여 적합을 진행하였습니다. 독립 변수로는 각 매체의 집행 금액을 이용하여 소진된 예산 금액이 사전예약자 평균의 변화에 얼만큼의 가중치를 갖는지 확인하였습니다.
Result
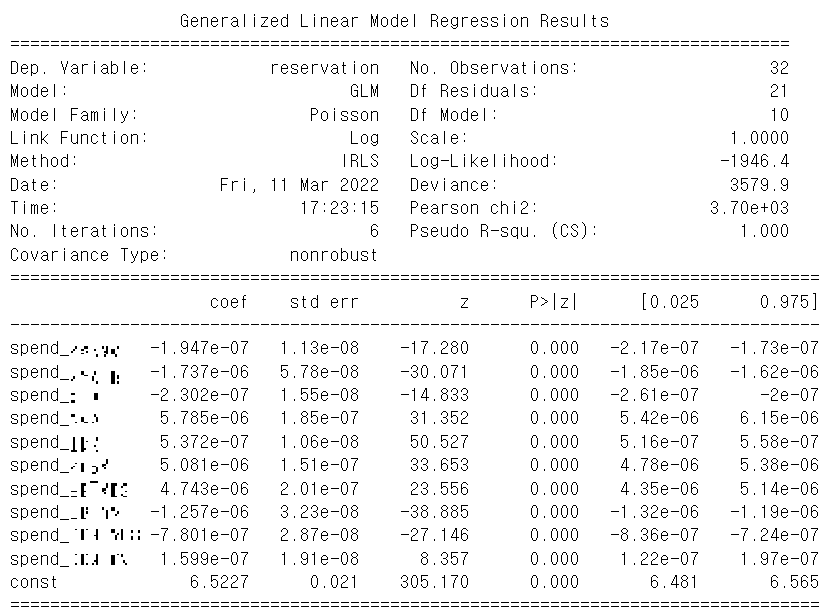
Poisson regression에서는 적합 결과가 link function인 log의 형태를 갖고 있기 때문에 각각의 coef에 exponential을 취해서 해석을 해야 합니다. 예를 들어서 한 매체의 coef인 -2.303e-7에 exponential을 취하면 0.999999769가 나오게 되며 이는 이 매체의 예산을 1원 늘렸을 때 사전 예약자가 0.999999769배 증가한다는 것입니다.
이 때 해석이 중요한데, 1보다 작은 가중치를 가졌다고 해서 “이 매체의 광고가 사전 예약 캠페인에 부정적인 영향을 미친 것이다”라고 해석하는 것은 옳지 않아 보입니다. 왜냐하면 모델의 특성 상 해당 가중치는 “타 매체들이 고정 되었을 때 이 매체의 예산이 변할 때의 사전 예약자 수의 변화”를 나타내는 것이고, 이 때 이 둘의 변화량은 선형적인 관계를 갖지 않기 때문입니다.
추가적으로 GLM 모델에서 한 독립 변수의 변화량은 종속 변수의 변화량의 평균치에 영향을 미치게 됩니다. 위의 예시에서 이 값이 1보다 작다면 부정적인 negative의 영향이 아닌 타 매체 대비 적은 평균치의 변화를 보였다는 것이고, 이를 해석하면 투입한 비용 대비 사전 예약자의 변화분이 평균치 보다 적다 즉, 비효율적으로 광고가 운영되었다는 것을 의미합니다.
따라서 위의 결과를 수치적으로 해석하는 것 이외에도 직관적으로 음의 coef를 갖는 매체는 투입한 비용 대비 효율적으로 사전 예약자의 변화에 기여하지 못했다고 해석할 수 있습니다.
각 매체의 비중을 시각적으로 표현하면 다음과 같습니다.
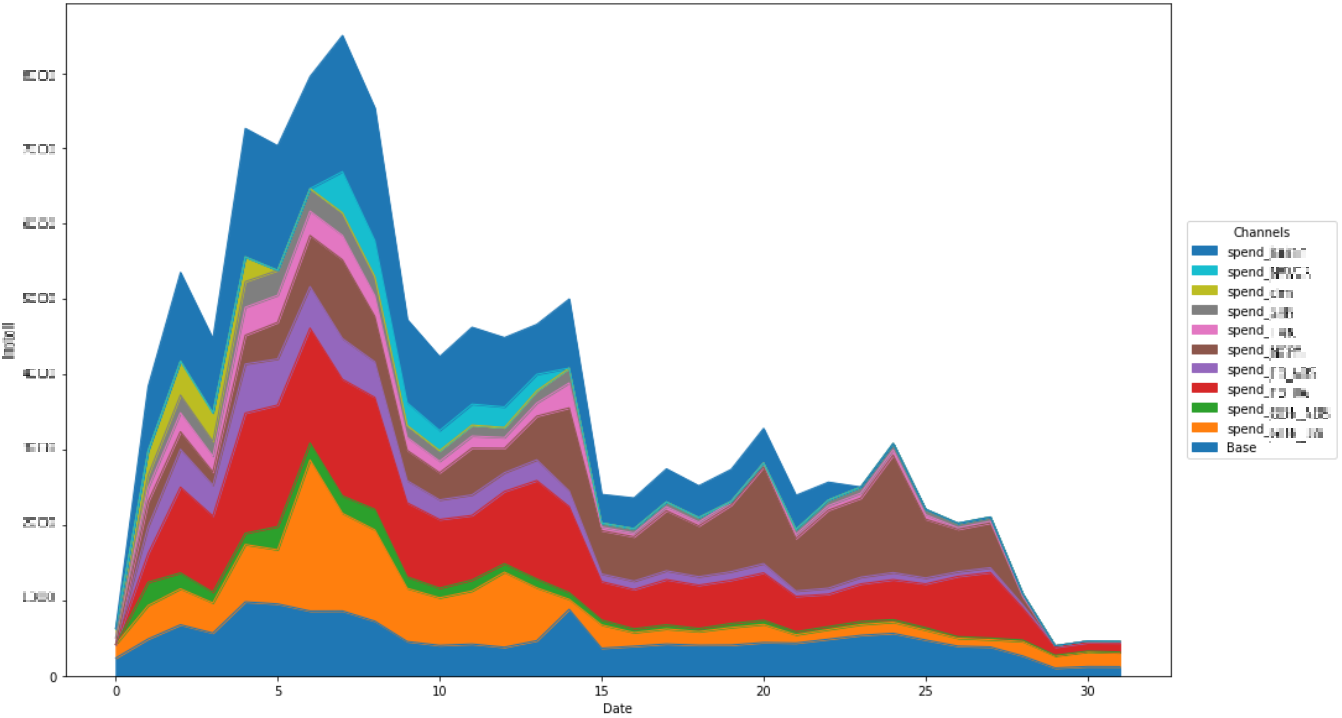
위의 그림은 각 매체의 비용에 가중치를 곱해주고 이 값의 합을 사전 예약자 수와 곱해준 결과를 표현한 것입니다.
이렇게 되면 각 매체가 가중치를 적용한 후, 이 가중치 비용에 따른 사전 예약자 비중을 파악할 수 있습니다.(비용을 많이 투입했는데 음의 가중치를 갖고 있다면 이것이 보정되어 나타나게 됩니다. 반대로 적은 수의 예산을 투입했더라도 큰 가중치를 갖고 있다면 이것이 보정 되어 사전 예약자에서 보다 높은 비중을 갖게 됩니다.)
그림의 가장 아래 부분의 Base는 모든 가중치가 0일 때 즉, 모든 광고 매체에 예산을 투입하지 않았을 때의 예상 사전 예약자 수를 나타냅니다. (GLM도 어쨌든 선형 모형의 일부분이기 때문에 선형 모형이 갖고 있는 단점을 갖고 있는데, 그 중 하나가 range의 한계입니다. 한마디로 “보지 못한 것은 알 수 없다” 입니다. 아무리 관측값들을 잘 설명한다고 하더라도 그 범위를 벗어나는 값에 대해서는 모델이 출력하는 값을 온전히 신뢰할 수 는 없습니다. 이번 캠페인에 이를 적용해보면 Base라는 것, 즉 이 모델의 y절편인 모든 캠페인이 중단되었을 때의 관측치는 없기 때문에 위의 결과만으로 해당 결과를 맹신하는 것은 금물입니다.)
그래프를 보았을 때 캠페인 중반 전에는 위쪽 파란색, 빨간색, 주황색이 비중 상위권을 차지하고 있는 것과 후반부에는 갈색과 빨간색이 높은 비중을 차지하고 있는 것을 확인할 수 있습니다.
다음으로는 일별 사전예약 비중의 총합과 예산 비중, 그리고 이 둘의 차이를 두어 효율적으로 진행된 매체는 어떤 것인지 살펴보았습니다.
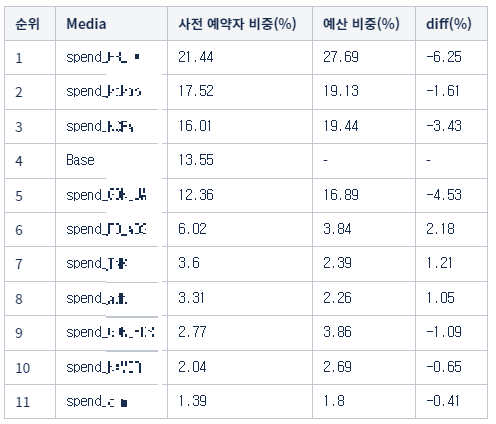
위의 표의 순위는 사전예약자 비중 순으로 나열되어 있습니다. 사전예약 비중은 예산 비중과 비교하여 그 효율성을 평가할 수 있습니다. 위에서 언급한 것처럼 높은 가중치를 갖는 매체일수록 투입된 예산 비중 대비 높은 사전 예약자 비중을 갖게 될 것입니다. 이는 사전예약자 비중에서 투입된 예산 비중에 대한 차이로 나타낼 수 있고 이것이 5번째 열의 diff로 나타나 있습니다.
Limitation
MMM을 해석할 때는 주의할 점이 하나 있습니다. 바로 Correlation, not Causation입니다. MMM을 통해서 우리는 다음과 같은 결론을 얻고 싶어합니다.
“매체 A의 광고비를 늘렸을 때, 얼마 만큼의 KPI 지표 상승이 기대되는가?”
하지만 이는 특정 조건이 만족한 상황에서만 가능한 해석입니다. 구글에서 발표한 논문인 D Chan(2017)을 살펴보면 MMM으로 위와 같은 인과 효과를 주장하기 위해서는 다음과 같은 조건이 필요하다고 합니다.
- 충분한 양의 데이터가 확보가 되어야 한다.
- 독립 변수들로 종속 변수의 상당 부분이 설명 가능해야 한다.
- 독립 변수들은 서로 독립이어야 한다.
- 독립 변수들의 충분한 변동성이 있어야 한다.
본 논문에서 충분한 양의 데이터란 parameter당 적어도 7-10개의 관측치가 필요하다고 말하고 있습니다. 또한, 2번은 Causal Inference 이론의 Local Average Treatment Effect(LATE)와 관련이 있어 보입니다. 그리고 당연한 얘기지만 내가 갖고 있는 독립 변수가 종속 변수를 충분히 설명할 수 있어야 인과 효과도 설명할 수 있으며, 독립 변수의 변동성이 적으면(예를 들어서 모든 날짜에 동일한 예산을 투입함) 모델이 인과 관계를 잡아내기 어렵다고 말하고 있습니다.
이러한 관점에서 보면 위의 결과는 아쉽게도 correlation의 단계를 벗어나지 못하고 있습니다. 이것은 아래의 두 가지 해석이 모두 가능하다는 의미가 됩니다.
- “광고 예산을 줄였기 때문에 사전 예약자 수가 감소했다”
- “사전 예약자 수가 감소했기 때문에 예산 절감을 위해 예산을 줄였다”
이는 실제 의사결정에 꽤나 많은 영향을 미치게 됩니다. 위의 결과를 예를 들면, 사전예약자 비중 순위 1위인 매체는 효율성의 측면에서는 가장 낮은 순위를 갖고 있습니다. 그렇다고 해서 위의 결과만으로는 “이 매체의 비중을 줄이고 사전예약 비중 순위가 6위인 매체의 예산 비중을 늘리면 더 효율적으로 광고가 집행될 것이다” 라고는 말할 수 없습니다. 즉, 아쉽게도 위의 결과로는 이번 캠페인에 대한 현상 해석만 가능할 뿐, 이 결과를 다음번 캠페인에 적극적으로 활용하기는 어렵습니다.
현재는 이러한 문제를 해결하고 인과 추론에 대한 당위성을 얻을 수 있는 방법을 위 논문의 조건에 근거하여 연구를 진행하고 있습니다.
-to be continued….